PROPOSED PROBLEMS
- Az ABC háromszögben
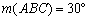 és
és 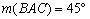 . Az AB és BC oldalakon vegyük fel az M és N pontokat úgy, hogy
. Az AB és BC oldalakon vegyük fel az M és N pontokat úgy, hogy 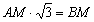 és
és 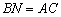 . Számítsd ki az NMB szög mértékét! (V:266, M.L. 1/2000)
. Számítsd ki az NMB szög mértékét! (V:266, M.L. 1/2000)
- Határozd meg az
összes olyan, egymástól különböző számjegyeket tartalmazó természetes számokat, amelyeknek a háromszorosát kapjuk, ha az első számjegyét utolsónak írjuk! (V:271, M.L. 1/2000)
- Az
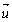 és
és 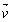 egységvektorok közös O kez
egységvektorok közös O kez dőpontja a d egyenesen helyezkedik el. Határozzuk meg az 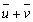 összegvektor végpontjának mértani helyét, ha d és O rögzítettek, az
összegvektor végpontjának mértani helyét, ha d és O rögzítettek, az 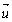 és a
és a 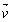 vektorok szöge nem kisebb, mint
vektorok szöge nem kisebb, mint 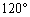 és d-hez viszonyítva
és d-hez viszonyítva 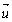 és
és 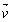 ugyanabban a félsíkban mozognak. (V:272, M.L. 1/2000)
ugyanabban a félsíkban mozognak. (V:272, M.L. 1/2000)
- Az ABC háromszög síkjában vegyük fel az M és N pontokat úgy, hogy az ABM
háromszög egyenlő oldalú legyen és teljesüljenek az 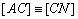 ,
, 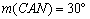 egyenlőségek (M és N az ABC háromszögön kívül helyezkednek el úgy, hogy az MAB, NAC és ABC háromszögeknek nincs közös belső pontjuk). Jelöljük K-val az MN szakasz felezőpontját. Bizonyítsátok be, hogy a BKC háromszög derékszögű. Hány fokosak a szögei? (Bege A. V:288, M.L. 3/2000)
Egy
egyenlőségek (M és N az ABC háromszögön kívül helyezkednek el úgy, hogy az MAB, NAC és ABC háromszögeknek nincs közös belső pontjuk). Jelöljük K-val az MN szakasz felezőpontját. Bizonyítsátok be, hogy a BKC háromszög derékszögű. Hány fokosak a szögei? (Bege A. V:288, M.L. 3/2000)
Egy 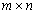 -es négyzetháló minden mezején egy-egy szöcske áll. Egy adott pillanatban minden szöcske átugrik egy csúcsosan szomszédos mezőre.
-es négyzetháló minden mezején egy-egy szöcske áll. Egy adott pillanatban minden szöcske átugrik egy csúcsosan szomszédos mezőre.
Bizonyítsd be, hogy ha m páros és n páratlan, akkor nem lehetséges, hogy az ugrások után is minden mezőn pontosan egy szöcske legyen!
Legalább hány mezőt kell a négyzethálóból kivágni ahhoz, hogy az ugrások után is minden mezőn pontosan egy szöcske állhasson? Hány különböző módon vághatók ki ezek a mezők?
(Bege A. V:289., M.L. 3/2000)
Egy szögmérőről egy szám kivételével mindegyik lekopott. Bizonyítsuk be, hogy ha a megmaradt szám 30-cal relatív prím, akkor e kopott szögmérő segítségével tudunk 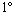 -os szöget mérni! (V:239. M.L.4/1999)
Bizonyítsd be, hogy ha az ABC hegyesszögű háromszög A-hoz tartozó magasságának és az AB, BC, CA oldalaknak a hosszai (ebben a sorrendben) egymás után következő természetes számok, akkor
-os szöget mérni! (V:239. M.L.4/1999)
Bizonyítsd be, hogy ha az ABC hegyesszögű háromszög A-hoz tartozó magasságának és az AB, BC, CA oldalaknak a hosszai (ebben a sorrendben) egymás után következő természetes számok, akkor 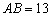 . (V:227, M.L. 3/1999)
Az
. (V:227, M.L. 3/1999)
Az 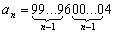 alakú számok közül melyek oszthatók 49-cel? (V:226., M.L. 3/1999)
Egy tetraéder éleire felírható-e az
alakú számok közül melyek oszthatók 49-cel? (V:226., M.L. 3/1999)
Egy tetraéder éleire felírható-e az 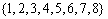 halmaz hat eleme úgy, hogy minden csúcsban ugyanannyi legyen a befutó élekre írt számok összege? (Bege A. V:228, M.L. 3/1999)
Hány különböző elemet tartalmazhat az
halmaz hat eleme úgy, hogy minden csúcsban ugyanannyi legyen a befutó élekre írt számok összege? (Bege A. V:228, M.L. 3/1999)
Hány különböző elemet tartalmazhat az 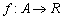 ,
, 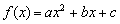 függvény képhalmaza, ha A egy n elemű számhalmaz, a, b, c valós számok és
függvény képhalmaza, ha A egy n elemű számhalmaz, a, b, c valós számok és 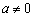 . (V:229., M.L. 3/1999)
Legyen A egy
. (V:229., M.L. 3/1999)
Legyen A egy 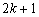 elemű való számokat tartalmazó halmaz. Bizonyítsuk be, hogy a k elemű részhalmazok legnagyobb elemeinek legkisebbike egyenlő ugyanazon részhalmazok legkisebb elemei közül a legnagyobbal! (V:221. M.L. 2/1999)
Az ABC háromszögben
elemű való számokat tartalmazó halmaz. Bizonyítsuk be, hogy a k elemű részhalmazok legnagyobb elemeinek legkisebbike egyenlő ugyanazon részhalmazok legkisebb elemei közül a legnagyobbal! (V:221. M.L. 2/1999)
Az ABC háromszögben 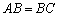 és
és 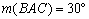 . Vegyük fel a háromszög síkjában a D pontot úgy, hogy
. Vegyük fel a háromszög síkjában a D pontot úgy, hogy 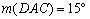 ,
, 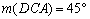 és AC-hez viszonyítva a B és D pontok ellentétes félsíkokban legyenek. Bizonyítsátok be, hogy
és AC-hez viszonyítva a B és D pontok ellentétes félsíkokban legyenek. Bizonyítsátok be, hogy 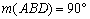 . (V:212. M.L. 1/1999)
Oldd meg a valós számok halmazán az
. (V:212. M.L. 1/1999)
Oldd meg a valós számok halmazán az 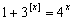 egyenletet! (V:150., M.L. 1/1998)
Fel lehet-e osztani 12 egymás utáni egész számot két hatos csoportba (
egyenletet! (V:150., M.L. 1/1998)
Fel lehet-e osztani 12 egymás utáni egész számot két hatos csoportba (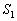 -be és
-be és 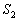 -be) úgy, hogy az
-be) úgy, hogy az 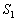 -ben levő elemek összege és négyzetösszege megegyezzen az
-ben levő elemek összege és négyzetösszege megegyezzen az 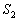 -beli elemek összegével illetve négyzetösszegével? (V:161., M.L. 2/1998)
Az ABC háromszög oldalaira (a háromszögön kívül) megszerkesztjük az ABMN, BCPQ és CATR hasonló téglalapokat
-beli elemek összegével illetve négyzetösszegével? (V:161., M.L. 2/1998)
Az ABC háromszög oldalaira (a háromszögön kívül) megszerkesztjük az ABMN, BCPQ és CATR hasonló téglalapokat 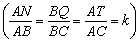 , majd az MBQU és RCPV paralelogrammákat. Bizonyítsd be, hogy ha az NU, TV és BC szakaszok felezőpontjai D, E és F, akkor az ADFE négyszög paralelogramma! (V:159. M.L. 2/1998)
Az
, majd az MBQU és RCPV paralelogrammákat. Bizonyítsd be, hogy ha az NU, TV és BC szakaszok felezőpontjai D, E és F, akkor az ADFE négyszög paralelogramma! (V:159. M.L. 2/1998)
Az 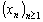 pozitív tagú sorozatról tudjuk, hogy teljesíti a
pozitív tagú sorozatról tudjuk, hogy teljesíti a 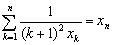 egyenlőséget, bármely
egyenlőséget, bármely 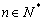 esetén. Határozzuk meg az
esetén. Határozzuk meg az 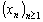 sorozat általános
sorozat általános 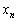 tagjának képletét n függvényében! (V:166. M.L. 3/1998)
Igazoljuk, hogy az ABCD négyszögben fennáll a következő egyenlőség:
tagjának képletét n függvényében! (V:166. M.L. 3/1998)
Igazoljuk, hogy az ABCD négyszögben fennáll a következő egyenlőség:
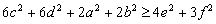 ,
,
ahol 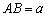 ,
, 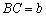 ,
, 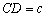 ,
, 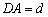 ,
, 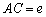 és
és 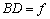 . (V:167. M.L. 3/1998)
. (V:167. M.L. 3/1998)
Ábrázoljuk az 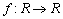 ,
, 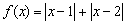 függvényt, majd bizonyítsuk be, hogy bármely
függvényt, majd bizonyítsuk be, hogy bármely 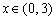 esetén, létezik olyan
esetén, létezik olyan 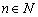 , amelyre
, amelyre 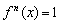 , ahol
, ahol 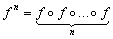 . (V: 185. M.L. 7/1998)
Az a és b pozitív valós számok teljesítik az
. (V: 185. M.L. 7/1998)
Az a és b pozitív valós számok teljesítik az 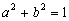 egyenlőséget. Igazold, hogy
egyenlőséget. Igazold, hogy 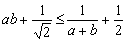 . (V:83. M.L. 1/1997)
Adott az
. (V:83. M.L. 1/1997)
Adott az 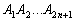 szabályos (2n+1) oldalú sokszög. Legyen M az
szabályos (2n+1) oldalú sokszög. Legyen M az 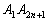 körív egy tetszőleges pontja. Igazold, hogy
körív egy tetszőleges pontja. Igazold, hogy 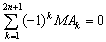 . (V:103. M.L. 3/1997)
Az ABC háromszögben
. (V:103. M.L. 3/1997)
Az ABC háromszögben 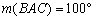 és
és 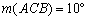 . Az AC és BC oldalakon vegyük fel az M és N pontokat úgy, hogy
. Az AC és BC oldalakon vegyük fel az M és N pontokat úgy, hogy 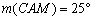 és
és 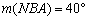 legyen. Számítsd ki az NMA szög mértékét! (V:104. M.L. 3/1997)
Adott az
legyen. Számítsd ki az NMA szög mértékét! (V:104. M.L. 3/1997)
Adott az 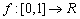 ,
, 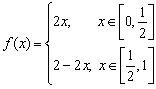 függvény. Számítsd ki az f n-edik iteráltját! (V:119. M.L. 7/1997)
Az ABC háromszögben az AB oldalt meghosszabbítjuk a
függvény. Számítsd ki az f n-edik iteráltját! (V:119. M.L. 7/1997)
Az ABC háromszögben az AB oldalt meghosszabbítjuk a 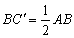 szakasszal. Az AM oldalfelező és a
szakasszal. Az AM oldalfelező és a 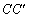 , valamint a BO és az AC egyenesek metszéspontját O-val, illetve
, valamint a BO és az AC egyenesek metszéspontját O-val, illetve 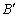 -vel jelöljük. Igazoljuk, hogy ha a
-vel jelöljük. Igazoljuk, hogy ha a 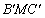 szög mértéke
szög mértéke 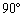 , akkor
, akkor 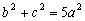 . Igaz-e az állítás fordítottja? (V:127. M.L. 8/1997)
Adott a d egyenes és az egyenesen egy O pont. Meghúzzuk az Ox és az Oy különböző félegyeneseket úgy, hogy a d-vel
. Igaz-e az állítás fordítottja? (V:127. M.L. 8/1997)
Adott a d egyenes és az egyenesen egy O pont. Meghúzzuk az Ox és az Oy különböző félegyeneseket úgy, hogy a d-vel 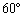 -os szögeket zárjanak be és d-hez viszonyítva ugyanabban a félsíkban legyenek. Ha A a d egy O-tól különböző tetszőleges pontja, B az A pontnak az Ox egyenesre, C a B pontnak az Oy egyenesre és D a C pontnak a d-re eső vetülete, valamint M és N az AC illetve a BD felezőpontja, számítsd ki az OMN szög mértékét! (V:124. M.L. 8/1997)
Helyettesítsük a betűket számjegyekkel úgy, hogy egy helyes műveletet kapjunk:
-os szögeket zárjanak be és d-hez viszonyítva ugyanabban a félsíkban legyenek. Ha A a d egy O-tól különböző tetszőleges pontja, B az A pontnak az Ox egyenesre, C a B pontnak az Oy egyenesre és D a C pontnak a d-re eső vetülete, valamint M és N az AC illetve a BD felezőpontja, számítsd ki az OMN szög mértékét! (V:124. M.L. 8/1997)
Helyettesítsük a betűket számjegyekkel úgy, hogy egy helyes műveletet kapjunk:
MATLAP+FELADAT=MEDVETÓ+10000
Határozd meg a 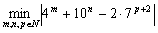 kifejezés értékét! (Kristály Sándor V:79. M.L. 10/1996)
Construct a continuous function
kifejezés értékét! (Kristály Sándor V:79. M.L. 10/1996)
Construct a continuous function 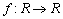 so that the equation
so that the equation 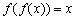 has an infinite number of roots while the equation
has an infinite number of roots while the equation 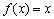 has only a finite number of roots. (Wildt József competition)
Let M be an interior point of the tetrahedron ABCD and let's denote by
has only a finite number of roots. (Wildt József competition)
Let M be an interior point of the tetrahedron ABCD and let's denote by 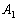 ,
, 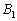 ,
, 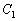 and
and 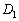 the following intersections
the following intersections 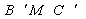 ,
, 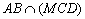 ,
, 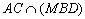 and
and 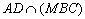 . Prove that if M is the centroid of the tetrahedron
. Prove that if M is the centroid of the tetrahedron 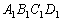 then
then 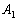 is the centroid of the BCD triangle and
is the centroid of the BCD triangle and 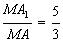 . (Wildt József competition)
The set
. (Wildt József competition)
The set 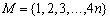 is given. Find a partition
is given. Find a partition 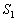 and
and 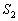 of the set M such that
of the set M such that 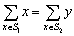 and
and 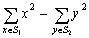 has maximal range. (O:871. Gazeta Matematică)
Fie ABCD un tetraedru oarecare şi M un punct în interiorul său. Planele BCM, CDM, şi respectiv DBM intersectează muchiile AD, AB şi AC respectiv în punctele
has maximal range. (O:871. Gazeta Matematică)
Fie ABCD un tetraedru oarecare şi M un punct în interiorul său. Planele BCM, CDM, şi respectiv DBM intersectează muchiile AD, AB şi AC respectiv în punctele 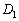 ,
, 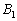 şi
şi 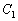 . Fie
. Fie 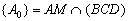 şi
şi 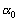 planul paralel cu planul BCD care trece prin A. Notând cu
planul paralel cu planul BCD care trece prin A. Notând cu 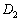 ,
, 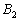 şi respectiv
şi respectiv 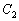 intersecţiile dreptelor
intersecţiile dreptelor 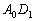 ,
, 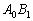 şi
şi 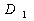 cu planul
cu planul 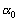 să se arate că A este centrul de greutate al triunghiului
să se arate că A este centrul de greutate al triunghiului 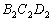 . (23862 Gazeta Matematică) (az n dimenziós változat a Nieuw Archief voor Wiskunde lapban jelent meg)
Legyen M a hegyesszögű ABC háromszög AD magasságának egy belső pontja és legyen
. (23862 Gazeta Matematică) (az n dimenziós változat a Nieuw Archief voor Wiskunde lapban jelent meg)
Legyen M a hegyesszögű ABC háromszög AD magasságának egy belső pontja és legyen 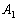 a háromszög köré írt kör A végpontú átmérőjének másik végpontja. A-ból az
a háromszög köré írt kör A végpontú átmérőjének másik végpontja. A-ból az 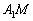 egyenesre emelt merőleges a BC egyenest
egyenesre emelt merőleges a BC egyenest 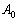 -ban metszi. Az M-ből AC-re illetve AB-re állított merőlegesek talppontjait jelölje rendre
-ban metszi. Az M-ből AC-re illetve AB-re állított merőlegesek talppontjait jelölje rendre 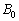 és
és 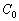 . Bizonyítsd be, hogy
. Bizonyítsd be, hogy 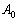 ,
, 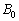 és
és 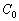 egy egyenesen vannak.
Az azonos körüljárású OAB, DOC és EFO háromszögek hasonlóak. Bizonyítsd be, hogy a BC, BE és FA szakaszok felezőpontjai az adottakhoz hasonló háromszöget határoznak meg. (47. Feladat, Mata 1995 május)
Bizonyítsd be, hogy bármely 2-nél nem kisebb természetes szám és tetszőleges
egy egyenesen vannak.
Az azonos körüljárású OAB, DOC és EFO háromszögek hasonlóak. Bizonyítsd be, hogy a BC, BE és FA szakaszok felezőpontjai az adottakhoz hasonló háromszöget határoznak meg. (47. Feladat, Mata 1995 május)
Bizonyítsd be, hogy bármely 2-nél nem kisebb természetes szám és tetszőleges 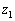 ,
, 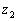 ,... ,
,... , 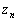 komplex számok esetén teljesül a
komplex számok esetén teljesül a 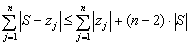 egyenlőtlenség, ahol
egyenlőtlenség, ahol 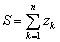 . (59. Feladat, Mata 1995 november)
Adott az
. (59. Feladat, Mata 1995 november)
Adott az 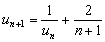 rekurziót teljesítő sorozat, ahol
rekurziót teljesítő sorozat, ahol 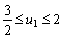 . Bizonyítsd be, hogy
. Bizonyítsd be, hogy 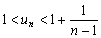 , ha
, ha 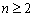 . (VI. Nemzetközi Magyar Matematika Verseny, 1997)
Let a, b and c positive real numbers. Prove that:
. (VI. Nemzetközi Magyar Matematika Verseny, 1997)
Let a, b and c positive real numbers. Prove that:
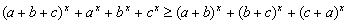 ,
,
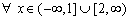 and for
and for 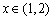 the reverse inequality holds.
the reverse inequality holds.
Let ABCDEF be a hexagon with M, N and P the midpoints of AD, BE and CF respectively. Prove that 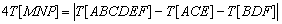 . (Mathematics Magazine)
Find a formula for
. (Mathematics Magazine)
Find a formula for 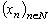 if
if 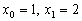 and
and 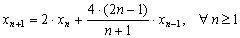 (Hegyi Lajos memorial contest, 1998)
The rule of generation of the next triangle is the same as the Pascal's triangle generation rule. Find a formula for the general term!
(Hegyi Lajos memorial contest, 1998)
The rule of generation of the next triangle is the same as the Pascal's triangle generation rule. Find a formula for the general term!
| |
|
|
|
|
1 |
|
|
|
|
|
| |
|
|
|
2 |
|
2 |
|
|
|
|
| |
|
|
3 |
|
4 |
|
3 |
|
|
|
| |
|
4 |
|
7 |
|
7 |
|
4 |
|
|
| |
5 |
|
11 |
|
14 |
|
11 |
|
5 |
|
|
6 |
|
16 |
|
25 |
|
25 |
|
16 |
|
6 |
Prove that if each of the equations 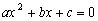 ,
, 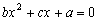 and
and 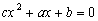 have an integer root, than this is a common root of these equations!
If the polynomial function
have an integer root, than this is a common root of these equations!
If the polynomial function 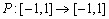 is defined by
is defined by 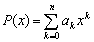 , then the maximum value of the
, then the maximum value of the 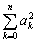 is attained for the nth Tshebyshev polynomial.
Az ABC háromszögben legyen
is attained for the nth Tshebyshev polynomial.
Az ABC háromszögben legyen 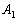 ,
, 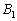 és
és 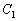 a BC oldalhoz írt körnek a megfelelő oldalakkal való érintési pontja és
a BC oldalhoz írt körnek a megfelelő oldalakkal való érintési pontja és 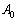 ennek a körnek a középpontja. Bizonyítsd be, hogy az
ennek a körnek a középpontja. Bizonyítsd be, hogy az 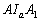 ,
, 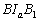 és
és 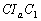 háromszögek köré írt körök középpontjai egy egyenesen vannak. (II. Székely Mikó Verseny 1992)
Létezik-e olyan
háromszögek köré írt körök középpontjai egy egyenesen vannak. (II. Székely Mikó Verseny 1992)
Létezik-e olyan 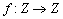 függvény, amelyre
függvény, amelyre 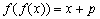 ,
, 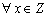 , ahol
, ahol 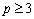 páratlan egész szám? (I. Bolyai János emlékverseny 1993)
Legyen ABC egy hegyesszögű háromszög és jelöljük T-vel az ABC háromszög Toricelli pontját. Igazold, hogy ABC pontosan akkor egyenlő oldalú, ha
páratlan egész szám? (I. Bolyai János emlékverseny 1993)
Legyen ABC egy hegyesszögű háromszög és jelöljük T-vel az ABC háromszög Toricelli pontját. Igazold, hogy ABC pontosan akkor egyenlő oldalú, ha 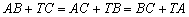 . (III. Wildt József verseny 1993)
Adott az ABC háromszög és
. (III. Wildt József verseny 1993)
Adott az ABC háromszög és 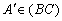 ,
, 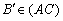 ,
, 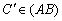 ,
, 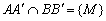 ,
, 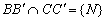 és
és 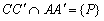 . Jelöljük
. Jelöljük 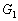 -gyel,
-gyel, 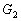 -vel és
-vel és 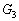 -mal az ABC háromszögek súlypontjait. Igazold, hogy a következő kijelentések egyenértékűek:
-mal az ABC háromszögek súlypontjait. Igazold, hogy a következő kijelentések egyenértékűek:
a) 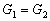 b)
b) 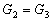 c)
c) 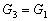 d)
d) 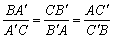
(Dene
ş Carol III. Wildt József verseny 1993)
Határozd meg azokat az 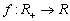 folytonos függvényeket, amelyekre
folytonos függvényeket, amelyekre
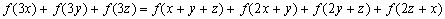 ,
, 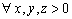
(III. Wildt József verseny 1993)
Az ABC háromszögben az 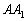 ,
, 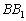 ,
, 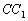 belső szögfelezők a háromszög köré írt kört az
belső szögfelezők a háromszög köré írt kört az 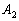 ,
, 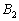 és
és 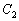 pontokban metszik. Igazold, hogy ha
pontokban metszik. Igazold, hogy ha 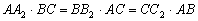 , akkor a háromszög egyenlő oldalú. (IV. Wildt József matematika verseny 1994)
Bizonyítsd be, hogy az
, akkor a háromszög egyenlő oldalú. (IV. Wildt József matematika verseny 1994)
Bizonyítsd be, hogy az 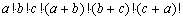 szorzat osztja a
szorzat osztja a 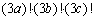 szorzatot, ha
szorzatot, ha 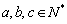 . (IV. Wildt József matematika verseny 1994)
Legyen
. (IV. Wildt József matematika verseny 1994)
Legyen 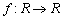 egy olyan függvény, amelyre
egy olyan függvény, amelyre 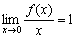 . Bizonyítsd be, hogy
. Bizonyítsd be, hogy 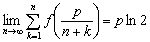 . (IV. Wildt József matematika verseny 1994)
Legyen
. (IV. Wildt József matematika verseny 1994)
Legyen 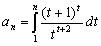 . Igazold, hogy létezik a
. Igazold, hogy létezik a 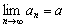 határérték és számítsd ki a
határérték és számítsd ki a 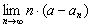 határértéket! (IV. Wildt József matematika verseny 1994)
Az ABC háromszögben jelöljük D-vel, E-vel és F-fel a BC oldalhoz írt kör érintési pontjait az oldalakkal, és
határértéket! (IV. Wildt József matematika verseny 1994)
Az ABC háromszögben jelöljük D-vel, E-vel és F-fel a BC oldalhoz írt kör érintési pontjait az oldalakkal, és 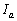 -val a kör középpontját. A DEF háromszögben a D szög belső szögfelezője az EF oldalt M-ben metszi. Igazold, hogy
-val a kör középpontját. A DEF háromszögben a D szög belső szögfelezője az EF oldalt M-ben metszi. Igazold, hogy 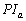 belső szögfelezője a
belső szögfelezője a 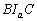 háromszögnek, ahol P-vel az AM és BC egyenesek metszéspontját jelöljük. (V. Wildt József matematika verseny 1995)
Adott az ABCD tetraéder és legyen M egy pont a térben. A tetraéder köré írt gömböt az AM, BM, CM és DM egyenesek az
háromszögnek, ahol P-vel az AM és BC egyenesek metszéspontját jelöljük. (V. Wildt József matematika verseny 1995)
Adott az ABCD tetraéder és legyen M egy pont a térben. A tetraéder köré írt gömböt az AM, BM, CM és DM egyenesek az 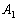 ,
, 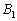 ,
, 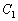 és
és 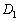 pontokban metszik. Határozd meg azon M belső pontok mértani helyét, amelyekre
pontokban metszik. Határozd meg azon M belső pontok mértani helyét, amelyekre 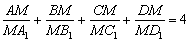 . (V. Wildt József matematika verseny 1995)
Legyen p egy prímszám és
. (V. Wildt József matematika verseny 1995)
Legyen p egy prímszám és 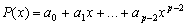 egy valós együtthatós polinom. Bizonyítsd be, hogy ha
egy valós együtthatós polinom. Bizonyítsd be, hogy ha 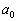 nem osztható p-vel és P-nek van egész gyöke, akkor a
nem osztható p-vel és P-nek van egész gyöke, akkor a 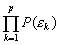 szorzat egész szám és p-nek többszöröse.(
szorzat egész szám és p-nek többszöröse.(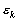 ,
, 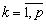 egységgyökök) (V. Wildt József matematika verseny 1995)
Az ABC háromszögben a B és C szögek belső szögfelezőinek talppontját
egységgyökök) (V. Wildt József matematika verseny 1995)
Az ABC háromszögben a B és C szögek belső szögfelezőinek talppontját 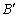 -tel és
-tel és 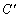 -tel, a külső szögfelező metszéspontját
-tel, a külső szögfelező metszéspontját 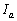 -val, míg a háromszög köré írt kör középpontját O-val jelöljük. Bizonyítsd be, hogy
-val, míg a háromszög köré írt kör középpontját O-val jelöljük. Bizonyítsd be, hogy 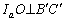 . (V. Nemzetközi Magyar Matematika Verseny, 1996)
Legyen D az ABC háromszög leghosszabb oldalának, a (BC)-nek egy tetszőleges pontja és
. (V. Nemzetközi Magyar Matematika Verseny, 1996)
Legyen D az ABC háromszög leghosszabb oldalának, a (BC)-nek egy tetszőleges pontja és 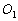 illetve
illetve 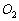 az ABD és ADC háromszögek köré írt körök középpontjai. E körökhöz a D pontban húzott érintők az AB és AC oldalakat E-ben, illetve F-ben metszik. Bizonyítsuk be, hogy az
az ABD és ADC háromszögek köré írt körök középpontjai. E körökhöz a D pontban húzott érintők az AB és AC oldalakat E-ben, illetve F-ben metszik. Bizonyítsuk be, hogy az 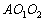 és
és 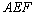 háromszögek hasonlók. (VI. Wildt József matematika verseny 1996)
Az ABCD négyszög síkjában vegyük fel az E és F pontokat úgy, hogy
háromszögek hasonlók. (VI. Wildt József matematika verseny 1996)
Az ABCD négyszög síkjában vegyük fel az E és F pontokat úgy, hogy 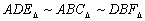 . Bizonyítsd be, hogy FCED paralelogramma. (VI. Wildt József matematika verseny 1996)
Bizonyítsd be, hogy egy hegyesszögű háromszög pontosan akkor egyenlő oldalú, ha
. Bizonyítsd be, hogy FCED paralelogramma. (VI. Wildt József matematika verseny 1996)
Bizonyítsd be, hogy egy hegyesszögű háromszög pontosan akkor egyenlő oldalú, ha 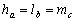 . (Bencze Mihály, VII. Wildt József verseny, 1997)
Az
. (Bencze Mihály, VII. Wildt József verseny, 1997)
Az 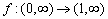 folytonos függvény teljesíti az
folytonos függvény teljesíti az 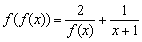 függvényegyenletet és
függvényegyenletet és 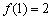 . Számítsd ki
. Számítsd ki 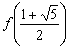 értékét és adjál példát ilyen függvényre. Hogyan változik
értékét és adjál példát ilyen függvényre. Hogyan változik 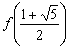 értéke, ha
értéke, ha 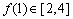 ?(Kovács Lajos, VII. Wildt József verseny, 1997)
Bizonyítsd be, hogy
?(Kovács Lajos, VII. Wildt József verseny, 1997)
Bizonyítsd be, hogy 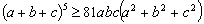 , ha a, b és c egy háromszög oldalhosszai. (Mata)
Bizonyítsd be, hogy
, ha a, b és c egy háromszög oldalhosszai. (Mata)
Bizonyítsd be, hogy 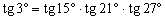 . (Szél Erika, 22980, M. L. 6/1993)
Bizonyítsd be, hogy
. (Szél Erika, 22980, M. L. 6/1993)
Bizonyítsd be, hogy 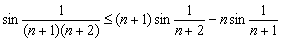 ,
,
any n >=1 (Egyenlőtlenségek, Gil Kiadó 1996)
Legyen O az ABC háromszög belső pontja és jelöljük 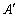 ,
, 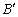 és
és  -tel az AO, BO és CO egyenesek metszéspontjait az BC, CA illetve BA oldalakkal. Bizonyítsd be, hogy ha
-tel az AO, BO és CO egyenesek metszéspontjait az BC, CA illetve BA oldalakkal. Bizonyítsd be, hogy ha 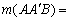
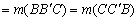 , akkor O az ABC háromszög ortocentruma. (V:14. M.L:2/1996)
Az OAB háromszögben
, akkor O az ABC háromszög ortocentruma. (V:14. M.L:2/1996)
Az OAB háromszögben 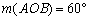 . Az OA és OB oldalakra, a háromszög külső tartományában megszerkesztjük az OPAC és OBD, A-ban illetve B-ben derékszögű háromszögeket, amelyeknek O-ban levő szögeik
. Az OA és OB oldalakra, a háromszög külső tartományában megszerkesztjük az OPAC és OBD, A-ban illetve B-ben derékszögű háromszögeket, amelyeknek O-ban levő szögeik 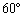 -osak. Ha M a CD szakasz felezőpontja, bizonyítsd be, hogy az AMB háromszög egyenlő oldalú. (V:18. M.L. 2/1996)
Adott a síkban három, egyenlő sugarú, egymást páronként az A, B és C pontokban érintő kör. Határozzuk meg azt a legnagyobb területű háromszöget, amelynek oldalegyenesei rendre átmennek az A, B és C pontokon, a csúcsai pedig rendre a körök belsejében vagy azok határán helyezkednek el. (V:29. M.L. 3/1996)
Két egységnyi oldalú szabályos hatszöget úgy helyezünk el a síkban, hogy az egyik hatszög középpontja a másik hatszög csúcsa legyen. Mekkora a két hatszög közös részének területe? (V:52. M.L. 7/1996)
Az ABCD egy tetszőleges O belső pontján át párhuzamosokat húzunk a négyzet oldalaihoz és átlóihoz. Bizonyítsd be, hogy a keletkezett nyolc síkrész közül minden másodiknak a területét összeadva a négyzet területének felét kapjuk. (V:60. M.L. 8/1996)
Az ABC háromszög BC és BA oldalait meghosszabbítjuk az
-osak. Ha M a CD szakasz felezőpontja, bizonyítsd be, hogy az AMB háromszög egyenlő oldalú. (V:18. M.L. 2/1996)
Adott a síkban három, egyenlő sugarú, egymást páronként az A, B és C pontokban érintő kör. Határozzuk meg azt a legnagyobb területű háromszöget, amelynek oldalegyenesei rendre átmennek az A, B és C pontokon, a csúcsai pedig rendre a körök belsejében vagy azok határán helyezkednek el. (V:29. M.L. 3/1996)
Két egységnyi oldalú szabályos hatszöget úgy helyezünk el a síkban, hogy az egyik hatszög középpontja a másik hatszög csúcsa legyen. Mekkora a két hatszög közös részének területe? (V:52. M.L. 7/1996)
Az ABCD egy tetszőleges O belső pontján át párhuzamosokat húzunk a négyzet oldalaihoz és átlóihoz. Bizonyítsd be, hogy a keletkezett nyolc síkrész közül minden másodiknak a területét összeadva a négyzet területének felét kapjuk. (V:60. M.L. 8/1996)
Az ABC háromszög BC és BA oldalait meghosszabbítjuk az 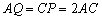 szakaszokkal (
szakaszokkal (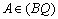 és
és 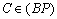 ). Hasonló módon vesszük fel az AB és AC oldalak meghosszabbításán az M illetve N pontot úgy, hogy
). Hasonló módon vesszük fel az AB és AC oldalak meghosszabbításán az M illetve N pontot úgy, hogy 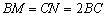 . Az MN és PQ szakaszok M-hez illetve Q-hoz közelebb eső harmadolópontjait R-rel és S-sel jelölve igazold, hogy az R, C és S pontok egy egyenesen vannak. (V:64. M.L. 8/1996)
Legyen
. Az MN és PQ szakaszok M-hez illetve Q-hoz közelebb eső harmadolópontjait R-rel és S-sel jelölve igazold, hogy az R, C és S pontok egy egyenesen vannak. (V:64. M.L. 8/1996)
Legyen 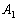 az A csúcs átmérősen ellentett pontja az ABC háromszög köré írt körön, D az A-ból húzott magasság talppontja és
az A csúcs átmérősen ellentett pontja az ABC háromszög köré írt körön, D az A-ból húzott magasság talppontja és 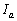 a BC oldalhoz írt kör középpontja. Ha
a BC oldalhoz írt kör középpontja. Ha 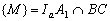 , igazold, hogy a
, igazold, hogy a 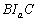 háromszögben
háromszögben 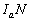 és
és 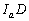 izogonálisak. (23289, M.L. 2/1995)
Legyen
izogonálisak. (23289, M.L. 2/1995)
Legyen 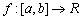 egy növekvő konvex függvény és
egy növekvő konvex függvény és  adott valós számok (
adott valós számok (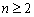 ). Bizonyítsd be, hogy
). Bizonyítsd be, hogy 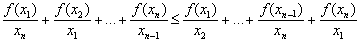 . (23294, M.L. 2/1995)
Az ABC háromszögben az
. (23294, M.L. 2/1995)
Az ABC háromszögben az  ,
,  és
és  egy pontban találkoznak. Bizonyítsd be, hogy ha
egy pontban találkoznak. Bizonyítsd be, hogy ha 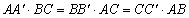 , akkor az
, akkor az 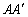 ,
, 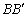 és
és 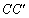 egyenesek magasságok. (E:11081, M.L. 10/1994)
Az ABC háromszögben az
egyenesek magasságok. (E:11081, M.L. 10/1994)
Az ABC háromszögben az 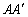 ,
, 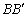 és
és 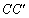 egyenesek egy pontban találkoznak (a háromszög belsejében). Bizonyítsd be, hogy ha az
egyenesek egy pontban találkoznak (a háromszög belsejében). Bizonyítsd be, hogy ha az 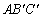 ,
, 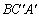 és
és 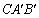 háromszögek egyenlő területűek, akkor az
háromszögek egyenlő területűek, akkor az 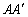 ,
, 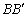 és
és 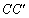 egyenesek oldalfelezők. (E:11074, M.L. 10/1994)
Legyen
egyenesek oldalfelezők. (E:11074, M.L. 10/1994)
Legyen 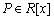 egyszeres és valós gyökökkel rendelkező polinom. Ha
egyszeres és valós gyökökkel rendelkező polinom. Ha 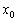 a derivált polinom egy gyöke, igazoljuk, hogy
a derivált polinom egy gyöke, igazoljuk, hogy 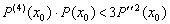 . (23244, M.L. 9/1994)
Bizonyítsd be, hogy ha a, b és c egy háromszög oldalhosszai, akkor
. (23244, M.L. 9/1994)
Bizonyítsd be, hogy ha a, b és c egy háromszög oldalhosszai, akkor
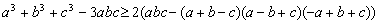
(23112, M.L. 3/1994)
Az ABC háromszögben 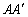 ,
, 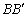 és
és 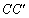 összefutó egyenesek. Legyen
összefutó egyenesek. Legyen 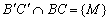 ,
, 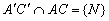 és
és 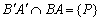 . Bizonyítsd be, hogy az
. Bizonyítsd be, hogy az 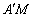 ,
, 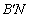 és
és 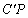 szakaszok felezőpontjai egy egyenesen vannak. (23040, M.L. 9/1993)
Igazoljuk, hogy minden háromszögben érvényes az
szakaszok felezőpontjai egy egyenesen vannak. (23040, M.L. 9/1993)
Igazoljuk, hogy minden háromszögben érvényes az
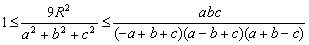
egyenlőtlenség. (22967, M.L.5/1993)
Jelöljük I-vel az ABC háromszögbe írt kör középpontját. Bizonyítsd be, hogy ha 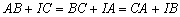 , akkor az ABC háromszög egyenlő szárú. (22941, M.L. 4/1993)
If
, akkor az ABC háromszög egyenlő szárú. (22941, M.L. 4/1993)
If 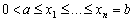 , prove that
, prove that
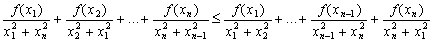 ,
,
where 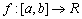 is increasing and concave. (PP89, Octogon 3(1995) No 1)
is increasing and concave. (PP89, Octogon 3(1995) No 1)
Let 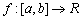 have Rolle properties on
have Rolle properties on 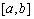 . Prove that there exist
. Prove that there exist 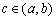 so that
so that
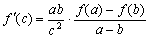
(PP 162, Octogon 3(1995), No. 2)
Prove that in every triangle we have 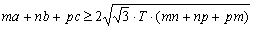 , where
, where 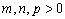 . (PP136, Octogon 3(1995), No 2)
Let n be an even positive integer. How many
. (PP136, Octogon 3(1995), No 2)
Let n be an even positive integer. How many 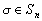 exists, for which
exists, for which 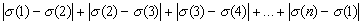 is maximal?
Let A be a
is maximal?
Let A be a 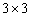 matrix with complex elements. Prove that if
matrix with complex elements. Prove that if 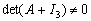 the following equivalence holds:
the following equivalence holds:
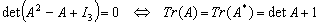
(PP. 1117, Octogon 7(1999), No 1)
proposed problem nr. 81
proposed problem nr. 82
proposed problem nr. 83
proposed problem nr. 84
proposed problem nr. 85
proposed problem nr. 86
proposed problem nr. 87
proposed problem nr. 88
proposed problem nr. 89
proposed problem nr. 90
proposed problem nr. 91
proposed problem nr. 92
proposed problem nr. 93
proposed problem nr. 94
proposed problem nr. 95
OPEN QUESTIONS
![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() és
és ![]() . (V:167. M.L. 3/1998)
. (V:167. M.L. 3/1998) függvény. Számítsd ki az f n-edik iteráltját! (V:119. M.L. 7/1997)
függvény. Számítsd ki az f n-edik iteráltját! (V:119. M.L. 7/1997)![]() ,
,![]() and for
and for ![]() the reverse inequality holds.
the reverse inequality holds.![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
![]() ,
, ![]()
![]()
![]()
![]() ,
,![]() is increasing and concave. (PP89, Octogon 3(1995) No 1)
is increasing and concave. (PP89, Octogon 3(1995) No 1)![]()
![]()