DOI: 10.24193/fpt-ro.2025.1.17

Authors: Gopi Prasad

Abstract: In this paper, we prove relational analogue of the Banach contraction principle in the settings of Menger probabilistic metric spaces under a Hadžić-type t-norm. In view of such investigations we obtain a Kelisky-Rivlin type results for a class of Bernstein type special operators introduced by Deo et. al. [Appl. Math. Comput. 201, (2008), 604-612] on the spaces of continuous functions 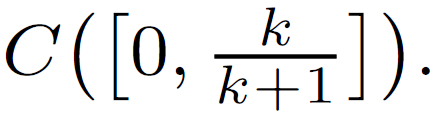Thus, such findings enrich, modify and generalize various prominent recent fixed point results of the existing literature.

Key Words and Phrases: Fixed point, Bernstein operator, contraction mapping.

2010 Mathematics Subject Classification: 47H10, 54H25.

Published on-line: February 1st, 2025.

Fulltext pdf

Back to volume's table of contents