DOI: 10.24193/fpt-ro.2025.1.09

Authors: Wenfeng Hu, Jingjing Wang and Xingyue He

Abstract: Under some conditions concerning the first eigenvalue corresponding to the relevant linear operator, the existence of nontrivial solutions and positive solutions for nonlinear fourth-order equation with Neumann boundary conditions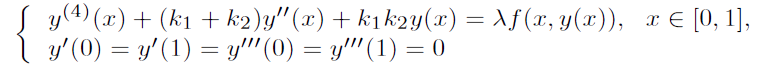



is obtained, where k₁ and k₂ are constants, ƒ ∈ C([0,1] × ℝ, ℝ ). And we discuss the properties of Green's function in detail according to the different classification of k₁ and k₂, an example is presented to illustrate the application of our main results. The main results are obtained by using the topological method and the fixed point theory of superlinear operators.

Key Words and Phrases: Euler-Bernoulli beam equations, fixed point, nontrivial and positive solutions, topological degree.

2010 Mathematics Subject Classification: 34B15, 34B18, 34B27, 34C23, 34G20.

Published on-line: February 1st, 2025.

Fulltext pdf

Back to volume's table of contents