Fixed Point Theory, Volume 25, No. 1, 2024, 43-60, February 1st, 2024
DOI: 10.24193/fpt-ro.2024.1.04
Authors:
María Laura de Borbón and Pablo Ochoa
Abstract: We deal with quasilinear elliptic problems with measure data:
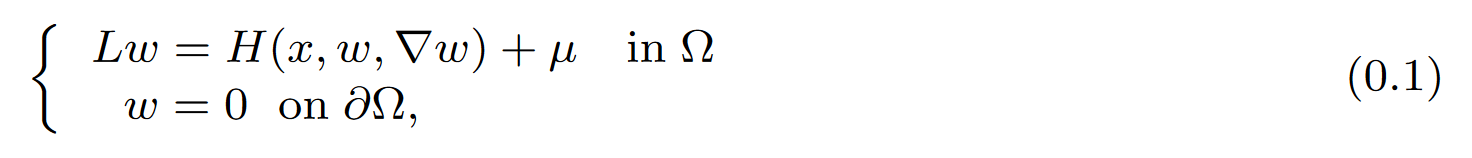
where Lw:=-div(A(x)∇w) with A=A(x) a bounded, coercive, and symmetric matrix field, the Hamiltonian H has at most q-growth in the gradient for 0<q<1, and μ is any Radon measure. We employ the compactness of the Green operator associated to L from the space of measures to W0{1, p}(Ω) for all p ∈ [1, N/(N-1)) together with fixed point arguments to solve problem (0.1) for any measure μ. Moreover, we provide explicit estimates of the solution in terms of the data. As an application, stability results are given. We also give conditions for the existence of W0{1, 2}-solutions through the classic theory of monotone and coercive operators. In any case, we do not impose any size restriction on μ and any sign condition on H.
Key Words and Phrases: Quasilinear elliptic equations, fixed point, Green's functions, weak solutions, uniqueness.
2010 Mathematics Subject Classification: 35J62, 47H10, 35J08, 35D30, 35A02.
Published on-line: February 1st, 2024.
Fulltext pdf
Back to volume's table of contents
|
_no__1.htm_cmp_axis010_bnr.gif)