DOI: 10.24193/fpt-ro.2023.1.20

Authors: Sourav Shil and Hemant Kumar Nashine

Abstract: In this study, we consider a non-linear matrix equation of the form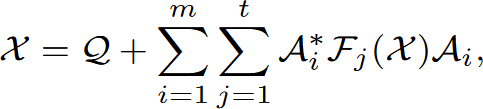



where 𝒬 is a Hermitian positive definite matrix, 𝒜_i^* stands for the conjugate transpose of an n × n matrix 𝒜_i and ℱ_j are order-preserving continuous mappings from the set of all Hermitian matrices to the set of all positive definite matrices such that ℱ(O)=O. We discuss sufficient conditions that ensure the existence of a unique positive definite solution of the given matrix equation. For this, we derive some fixed point results for Suzuki-implicit type mappings on metric spaces (not necessarily complete) endowed with arbitrary binary relation (not necessarily a partial order). We provide adequate examples to validate the fixed-point results and the importance of related work, and the convergence analysis of non-linear matrix equations.

Key Words and Phrases: Positive definite matrix, nonlinear matrix equation, fixed point, relational metric space, Suzuki contraction.

2010 Mathematics Subject Classification: 47H10, 54H25, 45J05.

Published on-line: February 1st, 2023.

Fulltext pdf

Back to volume's table of contents