DOI: 10.24193/fpt-ro.2021.1.13

Authors: J. Harjani, B. López and K. Sadarangani

Abstract: In this paper, by using a mixed monotone operator method we study the existence and uniqueness of positive solutions to the following nonlinear fractional boundary value problem

where 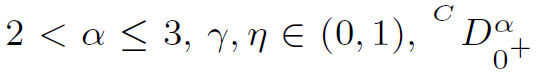denotes de Caputo fractional derivative, f : [0,1] × [0,∞) × [0,∞) → [0,∞) and g : [0,1] × [0,∞) → [0,∞) are continuous functions and H is an operator (not necessarily linear) applying 𝒞[0,1] into itself. Moreover, in order to illustrate our results, we present some examples.

Key Words and Phrases: Fractional boundary value problem, positive solution, mixed monotone operator, fixed point.

2010 Mathematics Subject Classification: 47H10, 49L20.

Published on-line: February 1st, 2021.

Abstract pdf          Fulltext pdf

Back to volume's table of contents