Hamming codes
Examples with Hamming codes
Contents
Generation of Hamming matrices
he command below exhibits the parity-check and generator matrices for a Hamming code with codeword length  and message length 4 = 7-3.
and message length 4 = 7-3.
format compact [h,g,n,k] = hammgen(3) msg=[1,0,1,0]; n=7; k=4; code = encode(msg,n,k,'linear/fmt',g) msgd = decode(code,n,k,'linear/fmt',g) % introduce an error perturbed_code = [0, 0, 1, 1, 0, 1, 0]; msgd2 = decode(perturbed_code,n,k,'linear/fmt',g) % minimum distance wt = gfweight(g,'gen') wt = gfweight(h,'par')
h =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
g =
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
n =
7
k =
4
code =
0 0 1 1 0 1 0
msgd =
1 0 1 0
msgd2 =
1 0 1 0
wt =
3
wt =
3
Haming example
The command below, which uses $1 + x^2 + x^33 as the primitive polynomial for GF(23), shows that the parity-check matrix depends on the choice of primitive polynomial. Notice that h1 below is different from h in the example above.
[h1,g1,n1,k1] = hammgen(3,[1 0 1 1]) wt = gfweight([1 0 1 1],n)
h1 =
1 0 0 1 1 1 0
0 1 0 0 1 1 1
0 0 1 1 1 0 1
g1 =
1 0 1 1 0 0 0
1 1 1 0 1 0 0
1 1 0 0 0 1 0
0 1 1 0 0 0 1
n1 =
7
k1 =
4
wt =
3
gen2par
Convert between parity-check and generator matrices The standard forms of the generator and parity-check matrices for an [n,k] binary linear block code are shown in the table below
h = gen2par(g) g1 = gen2par(h1)
h =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
g1 =
1 0 1 1 0 0 0
1 1 1 0 1 0 0
1 1 0 0 0 1 0
0 1 1 0 0 0 1
| Type of Matrix | Standard Form | Dimensions |
| Generator | [Ik P] or [P Ik] | k-by-n |
| Parity-check | [-P' In-k] or [In-k -P' ] | (n-k)-by-n |
We check

mod(g*h',2)
ans =
0 0 0
0 0 0
0 0 0
0 0 0
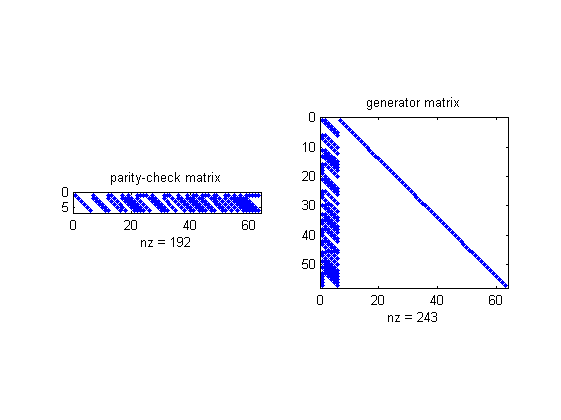
Haming example for magnetic tape
57 x 63 matrix G and a 63 x 6 matrix H
[h2,g2,n2,k2] = hammgen(6); n2,k2 subplot(1,2,1) spy(h2) title('parity-check matrix') subplot(1,2,2) spy(g2) title('generator matrix')
n2 =
63
k2 =
57